Logaritma
Soal Nomor 1
Penyelesaian dari $^2 \log (2x-5) = 4$ adalah $x = \cdots \cdot$
A. $5\dfrac12$ D. $10\dfrac14$
B. $7\dfrac12$ E. $10\dfrac12$
C. $8\dfrac12$
Diketahui $^{\color{red}{2}} \log (\color{blue}{2x-5}) = \color{red}{4}.$
Dengan mengubah bentuk logaritma di atas menjadi bentuk pangkat, kita akan memperoleh
$$\begin{aligned} \color{blue}{2x-5} & =\color{red}{2^4} \\ 2x-5 & = 16 \\ 2x & = 16 + 5 \\ 2x & = 21 \\ x & = \dfrac{21}{2} = 10\dfrac12 \end{aligned}$$Jadi, penyelesaian persamaan logaritma tersebut adalah $\boxed{x = 10\dfrac12}$
(Jawaban E)
Soal Nomor 2
Penyelesaian dari $^4 \log (3x-1) = 2$ adalah $x = \cdots \cdot$
A. $5\dfrac13$ D. $7\dfrac23$
B. $5\dfrac23$ E. $9\dfrac13$
C. $7\dfrac13$
Diketahui $^{\color{red}{4}} \log (\color{blue}{3x-1}) = \color{red}{2}.$
Dengan mengubah bentuk logaritma di atas menjadi bentuk pangkat, kita akan memperoleh
$$\begin{aligned} \color{blue}{3x-1} & =\color{red}{4^2} \\ 3x-1 & = 16 \\ 3x & = 16 + 1 \\ 3x & = 17 \\ x & = \dfrac{17}{3} = 5\dfrac23 \end{aligned}$$Jadi, penyelesaian persamaan logaritma tersebut adalah $\boxed{x = 5\dfrac23}$
(Jawaban B)
Soal Nomor 3
Himpunan penyelesaian dari $^3 \log (x^2+x+15) = 3$ adalah $\cdots \cdot$
A. $\{-4, -3\}$ D. $\{-3, 4\}$
B. $\{-4, 3\}$ E. $\{3, 4\}$
C. $\{-3, 3\}$
Diketahui $^{\color{red}{3}} \log (\color{blue}{x^2+x+15}) = \color{red}{3}.$
Dengan mengubah bentuk logaritma di atas menjadi bentuk pangkat, kita akan memperoleh
$$\begin{aligned} \color{blue}{x^2+x+15} & =\color{red}{3^3} \\ x^2+x+15 & = 27 \\ x^2+x-12 & = 0 \\ (x+4)(x-3) & = 0 \\ x = -4~\text{atau}~x & = 3 \end{aligned}$$Jadi, himpunan penyelesaian persamaan logaritma tersebut adalah $\boxed{\{-4, 3\}}$
(Jawaban B)
Soal Nomor 4
Jumlah akar-akar dari persamaan $\log (x^2-1) = \log 8$ adalah $\cdots \cdot$
A. $-6$ C. $0$ E. $6$
B. $-3$ D. $3$
Perhatikan bahwa
$$\begin{aligned} \cancel{\log} (x^2-1) & = \cancel{\log} 8 \\ x^2-1 & = 8 \\ x^2-9 & = 0 \\ (x+3)(x-3) & = 0 \\ x_1 = -3~\text{atau}~x_2 & = 3 \end{aligned}$$Jadi, jumlah akar-akar dari persamaan logaritma tersebut adalah $\boxed{x_1+x_2 = (-3)+3 = 0}$
(Jawaban C)
Soal Nomor 5
Penyelesaian dari persamaan $^x \log (4x + 12) = 2$ adalah $\cdots \cdot$
A. $x = -6$ D. $x = 6$
B. $x = -2$ E. $x = -2$ atau $x = 6$
C. $x = 2$
Diketahui $^x \log (4x + 12) = 2$.
Dengan mengubah bentuk logaritma di atas menjadi bentuk pangkat, kita akan memperoleh
$$\begin{aligned} x^2 & = 4x + 12 \\ x^2-4x-12 & = 0 \\ (x-6)(x+2) & = 0 \\ x = 6~\text{atau}~x &= -2 \end{aligned}$$Cek syarat bahwa basis harus positif dan tidak sama dengan $1$. Perhatikan bahwa substitusi $x = -2$ membuat basis bertanda negatif sehingga penyelesaian ini ditolak.
Jadi, penyelesaian persamaan logaritma tersebut hanya $\boxed{x = 6}$
(Jawaban D)
Soal Nomor 6
Nilai $x$ yang memenuhi persamaan $\log \sqrt{^2 \log x + 8} = 1$ adalah $\cdots \cdot$
A. $2^{82}$ C. $2^{90}$ E. $4^{92}$
B. $2^{84}$ D. $2^{92}$
Ingat bahwa prinsip logaritma adalah: $a^c = b \iff ^a \log b = c$.
Untuk itu, diperoleh
$$\begin{aligned} \log \sqrt{^2 \log x + 8} & = 1 \\ {\log} \sqrt{^2 \log x + 8} & = {\log} 10 \\ \sqrt{^2 \log x + 8} & = 10 \\ ^2 \log x + 8 & = 100 && (\text{Kuadratkan kedua ruas}) \\ ^2 \log x & = 92 \\ x &= 2^{92} \end{aligned}$$Jadi, nilai $x$ yang memenuhi persamaan tersebut adalah $\boxed{x = 2^{92}}$
(Jawaban D)
Soal Nomor 7
Nilai $x$ yang memenuhi $^x \log \left(\dfrac{2}{9}\right)^3 =-2$ adalah $\cdots \cdot$
A. $\dfrac{27}{2}$ D. $\dfrac{27}{4}\sqrt2$
B. $\dfrac{27}{4}$ E. $\dfrac{27}{8}\sqrt2$
C. $\dfrac{27}{2}\sqrt2$
Berdasarkan hubungan pangkat dan logaritma beserta sifat-sifat eksponen, kita dapatkan
$\begin{aligned} x^{-2} & = \left(\dfrac{2}{9}\right)^3 \\ (x^{-2})^{-\frac{1}{2}} & = \left(\left(\dfrac{2}{9}\right)^3\right)^{-\frac{1}{2}} \\ x & = \left( \dfrac{9}{2}\right)^{\frac{3}{2}} = \dfrac{27}{2\sqrt{2}} = \dfrac{27}{4}\sqrt{2} \end{aligned}$
Jadi, nilai dari $\boxed{x = \dfrac{27}{4}\sqrt{2}}$
(Jawaban D)
Soal Nomor 8
Jika $a$ memenuhi persamaan $^2 \log 2x + \! ^3 \log 3x = \! ^4 \log 4x^2$, maka $^a \log 3 = \cdots \cdot$
A. $-3$ C. $-1$ E. $2$
B. $-2$ D. $1$
Diketahui $^2 \log 2x + \! ^3 \log 3x = \! ^4 \log 4x^2.$
Persamaan di atas dapat kita tuliskan menjadi
$$\begin{aligned} ^2 \log 2x + (^3 \log 3 + \! ^3 \log x) & = \! ^4 \log (2x)^2 \\ {^2 \log 2x} + (1 + \! ^3 \log x) & = \! {^2 \log 2x} \\ 1 + \! ^3 \log x & = 0 \\ ^3 \log x & = -1 \\ x & = 3^{-1} \end{aligned}$$Jadi, nilai $a = 3^{-1}$ sehingga $\boxed{^a \log 3 = \! ^{3^{-1}} \log 3 = -1}$
(Jawaban C)
Soal Nomor 9
Jika $^4 \log \! ^4 \log x-^4 \log \! ^4 \log \! ^4 \log 16 = 2$, maka $x = \cdots \cdot$
A. $4^2$ C. $4^8$ E. $4^{32}$
B. $4^4$ D. $4^{16}$
Perhatikan bahwa
$$\begin{aligned} ^4 \log \! ^4 \log x- \! ^4 \log \! ^4 \log \! ^4 \log 16 & = 2 \\ ^4 \log \! ^4 \log x- \! ^4 \log \! ^4 \log 2 & = 2 \\ ^4 \log \! ^4 \log x- \! ^4 \log \dfrac{1}{2} & = 2 \\ ^4 \log \! ^4 \log x- \! ^{2^2} \log 2^{-1} & = 2 \\ ^4 \log \! ^4 \log x + \dfrac{1}{2} & = 2 \\ ^4 \log \! ^4 \log x & = \dfrac{3}{2} \\ ^4 \log x & = 4^{\frac{3}{2}} = (2^2)^{\frac{3}{2}} = 8 \\ x & = 4^8 \end{aligned}$$Jadi, nilai dari $x$ adalah $\boxed{x = 4^8}$
(Jawaban C)
Soal Nomor 10
Salah satu nilai $p$ yang memenuhi $$4 \cdot \! ^{p} \log 2-^2 \log p^2 = -7$$adalah $\cdots \cdot$
A. $2$ C. $8$ E. $32$
B. $4$ D. $16$
Pada bentuk logaritma, posisi basis dan numerus dapat dibalik dengan menggunakan sifat
$$^a \log b = \! \dfrac{1}{^b \log a}.$$Oleh karena itu, persamaan di atas dapat ditulis menjadi
$$4 \cdot \dfrac{1}{^{2} \log p}-2 \cdot \! ^2 \log p = -7$$Sekarang, misalkan $^2 \log p = x$ sehingga kita peroleh
$$\begin{aligned} \dfrac{4}{x}-2x & = -7 \\ \text{Kalikan kedua ruas}&~\text{dengan}~x \\ 4-2x^2 & = -7x \\ 2x^2-7x-4 & = 0 \\ (2x+1)(x-4) & = 0 \\ x = -\dfrac12~\text{atau}~&x = 4 \end{aligned}$$Substitusi balik dan kita peroleh
$$\begin{aligned} ^2 \log p = -\dfrac12 & \Rightarrow p = 2^{-1/2} \\ ^2 \log p = 4 & \Rightarrow p = 2^4 = 16 \end{aligned}$$Jadi, salah satu nilai $p$ yang memenuhi persamaan adalah $\boxed{p=16}$
(Jawaban D)
Soal Nomor 11
Nilai $x$ yang memenuhi persamaan $\dfrac{x^{\log 15x}} {27x^{\log 5x}} = 9$ adalah $\cdots \cdot$
A. $1.000$ D. $1.000.000$
B. $10.000$ E. $10.000.000$
C. $100.000$
Dengan menggunakan sifat pangkat dan logaritma, diperoleh
$\begin{aligned} \dfrac{x^{\log 15x}} {27x^{\log 5x}} & = 9 \\ \dfrac{1}{27} \times \dfrac{x^{\log 15x}} {x^{\log 5x}} & = 9 \\ x^{\log 15x-\log 5x} & = 9 \times 27 \\ x^{\log \frac{15\cancel{x} } {5\cancel{x}}} & = 3^2 \times 3^3 \\ x^{\log 3} & = 3^5 \end{aligned}$
Berdasarkan hubungan pangkat dan logaritma, bentuk terakhir dapat ditulis $\begin{aligned} ^x \log 3^5 & = \log 3 \\ ^x \cancel{\log 3^5} & = ^{10^5} \cancel{\log 3^5}\\ x & = 10^5 = 100.000\end{aligned}$
Jadi, nilai $x$ yang memenuhi persamaan tersebut adalah $\boxed{x = 100.000}$
(Jawaban C)
Soal Nomor 12
Hasil kali semua nilai $x$ yang memenuhi persamaan $\dfrac{x^2}{10.000} = \dfrac{10.000}{x^{2(^{10} \log x)-8}}$ adalah $\cdots \cdot$
A. $100$ D. $100.000$
B. $1.000$ E. $1.000.000$
C. $10.000$
Dengan menggunakan sifat-sifat eksponen dan logaritma, kita peroleh
$$\begin{aligned} \dfrac{x^2}{10.000} & = \dfrac{10.000}{x^{2(^{10} \log x)-8}} \\ x^{2 + 2 \log x-8} & = 10.000 \cdot 10.000 \\ x^{2 \log x-6} & = 10^8 \\ (x^{\log x-3})^2 & = (10^4)^2 \\ x^{\log x-3} & = 10^4 \\ \text{Tarik logarit}\text{ma di}&~\text{kedua ruas} \\ \log x^{\log x-3} & = \log 10^4 \\ (\log x-3)(\log x) & = 4 \\ \log^2 x-3 \log x-4 & = 0 \\ (\log x-4)(\log x+1) & = 0 && (\text{Difaktorkan}) \\ \log x = 4~\text{atau}~&\log x = -1 \end{aligned}$$Dengan demikian, didapat
$$\begin{aligned} \log x = 4 & \Rightarrow x_1 = 10^4 \\ \log x = -1 & \Rightarrow x_2 = 10^{-1} \end{aligned}$$Jadi, hasil kali semua nilai $x$ dari persamaan logaritma tersebut adalah $$\boxed{x_1x_2 = 10^4 \cdot 10^{-1} = 10^3 = 1.000}$$ (Jawaban B)
Soal Nomor 13
Jika $6(3^{40})(^2 \log a) + 3^{41}(^2 \log a) = 3^{43}$, maka nilai $a = \cdots \cdot$
A. $2$ C. $8$ E. $16$
B. $3$ D. $9$
Dengan menggunakan sifat pangkat dan logaritma, diperoleh
$$\begin{aligned} 6(3^{40})(^2 \log a) + 3^{41}(^2 \log a) & = 3^{43} \\ 2.3(3^{40})(^2 \log a) + 3^{41}(^2 \log a) & = 3^{41} \cdot 3^2 \\ 2\cancel{(3^{41})}(^2 \log a) + \cancel{3^{41}}(^2 \log a) & = \cancel{3^{41}} \cdot 9 \\ 2(^2 \log a) + \! ^2 \log a & = 9 \\ 3(^2 \log a) & = 9 \\ ^2 \log a & = \dfrac{9}{3}=3 \\ a & = 2^3 = 8 \end{aligned}$$Jadi, nilai $a$ adalah $\boxed{8}$
(Jawaban C)
Soal Nomor 14
Nilai $x$ yang memenuhi $8^{x+1} = 24^{x-1}$ adalah $a \cdot ^3 \log 2 + b$ dengan $a, b$ bilangan bulat positif. Nilai dari $a + b = \cdots \cdot$
A. $3$ C. $6$ E. $9$
B. $5$ D. $7$
Persamaan berpangkat tersebut tidak dapat diselesaikan dengan cara standar karena $8$ dan $24$ tidak memiliki basis pangkat yang sama.
Logaritmakan kedua ruas, kemudian gunakan sifat-sifat logaritma untuk mencari nilai $x$ sebagai berikut.
$$\begin{aligned} 8^{x+1} & = 24^{x-1} \\ \log 8^{x+1} & = \log 24^{x-1} \\ (x+1) \log 8 & = (x-1) \log 24 \\ x \log 8 + \log 8 & = x \log 24-\log 24 \\ x \log 8- x \log 24 & =-\log 24-\log 8 \\ x(\log 8-\log 24) & =-\log 24-\log 8 \\ x & = \dfrac{-\log 24-\log 8}{\log 8-\log 24} = \dfrac{\log 24 + \log 8}{\log 24-\log 8} \\ x & = \dfrac{\log (8 \times 3) + \log 8}{\log \frac{24}{8}} \\ x & = \dfrac{\log 8 + \log 3 + \log 8}{\log 3} \\ x & = \dfrac{2 \log 8 + \log 3}{\log 3} \\ x & = \dfrac{2 \log 2^3 + \log 3}{\log 3} \\ x & = \dfrac{6 \log 2 + \log 3}{\log 3} \\ x & = \dfrac{6 \log 2}{\log 3} + \dfrac{\log 3}{\log 3} \\ x & = 6 \cdot \! ^3 \log 2 + 1 \end{aligned}$$Jadi, nilai $x$ yang memenuhi persamaan berpangkat di atas adalah $\boxed{x = 6 \cdot \! ^3 \log 2 + 1}$ sehingga $a = 6$ dan $b = 1$, dan itu artinya, $\boxed{a + b = 6 + 1 = 7}$
(Jawaban D)
Soal Nomor 15
Persamaan $$^{x^2-6x+14} \log (x-3) = \! ^{4x^2-4x+1} \log (x^2-6x+9)$$ akan bernilai benar apabila nilai $x$ adalah $\cdots \cdot$
A. $3$ D. $3$ atau $4$
B. $5$ E. $4$ atau $5$
C. $3$ atau $5$
Perhatikan ruas kanan persamaan tersebut. Dengan menggunakan sifat bahwa $\boxed{a^n \log b^n = \! ^a \log b}$, diperoleh
$$\begin{aligned} ^{4x^2-4x+1} \log (x^2-6x+9) & = \! ^{(2x-1)^2} \log (x-3)^2 \\ & = \! ^{2x-1} \log (x-3) \end{aligned}$$ Kasus 1: Kesamaan Numerus, Ambil Basisnya
Persamaan logaritma yang diberikan dapat ditulis sebagai berikut.
$$\begin{aligned} ^{x^2-6x+14} \cancel{\log (x-3)} & = \! ^{2x-1} \cancel{\log (x-3)} \\ x^2-6x+14 & = 2x-1 \\ x^2-8x + 15 & = 0 \\ (x-3)(x-5) & = 0 \end{aligned}$$Diperoleh $x = 3$ atau $x = 5.$
Sekarang, ingat bahwa numerus logaritma haruslah positif sehingga $x-3 > 0 \iff \boxed{x > 3}$
Kasus 2: Numerus = 1
Persamaan logaritma
$$^{x^2-6x+14} \log (x-3) = \! ^{2x-1} \log (x-3)$$memiliki numerus yang sama sehingga nilai variabel yang mungkin memenuhi didapat ketika numerusnya dibuat sama dengan $1$, yaitu $x-3 = 1 \Leftrightarrow x=4.$
Substitusi $x=4$ pada basis $x^2-6x+14$ dan $2x-1$ menghasilkan bilangan positif yang tidak sama dengan $1$ (syarat basis pada logaritma) sehingga $x=4$ juga memenuhi persamaan.
Untuk itu, disimpulkan bahwa $x = 4$ atau $x = 5$ akan membuat persamaan tersebut bernilai benar.
(Jawaban E)
Soal Nomor 16
Jika $u=x^2$ dan $^x \log 10 = \! ^u \log (5u-40),$ maka nilai $u$ adalah $\cdots \cdot$
A. $25$ C. $27$ E. $29$
B. $26$ D. $28$
Substitusikan $u=x^2$ pada persamaan logaritma tersebut.
$\begin{aligned} ^x \log 10 & = \! ^u \log (5u-40) \\ ^x \log 10 & = \! ^{x^2} \log (5u-40) \\ ^x \log 10 & = \dfrac{1}{2} \cdot \! ^x \log (5u-40) \\ \bcancel{^x \log} 10 & = \bcancel{^x \log} \sqrt{5u-40} \\ 10 & = \sqrt{5u-40} \\ \text{Kuadratkan}~&\text{kedua ruas} \\ 10^2 & = (\sqrt{5u-40})^2 \\ 100 & = 5u-40 \\ 140 & = 5u \\ u & = \dfrac{140}{5} = 28 \end{aligned}$
Jadi, nilai $u$ adalah $\boxed{28}$
(Jawaban D)
Soal Nomor 17
Jika $x \log 2- y \log 3 + z \log 5 = 10$ maka $2x + 8y-3z = \cdots \cdot$
A. $-20$ C. $0$ E. $20$
B. $-10$ D. $10$
Dengan menggunakan sifat logaritma, diperoleh
$\begin{aligned} x \log 2-y \log 3 + z \log 5 & = 10 \\ \log 2^x-\log 3^y + \log 5^z & = 10 \\ \cancel{\log} \left(\dfrac{2^x \cdot 5^z} {3^y}\right) & = \cancel{\log} 10^{10} \\ \dfrac{2^x \cdot 5^z} {3^y} & = 10^{10} \end{aligned}$
Karena $2, 3, 5$ merupakan bilangan prima, maka bentuk pecahan $\dfrac{2^x \cdot 5^z} {3^y}$ sudah dalam bentuk paling sederhana. Ini berarti $3^y$ haruslah bernilai $1$ (jika tidak, hasilnya akan berupa pecahan).
Jadi, $y$ yang memenuhi adalah $0$.
Untuk itu, $2^x \cdot 5^z = 10^{10}$.
Pilih $x = z = 10$ sehingga
$2^{10} \cdot 5^{10} = (2 \cdot 5)^{10} = 10^{10}$.
Jadi, hasil dari
$\boxed{\begin{aligned} 2x + 8y-3z & = 2(10) + 8(0)- 3(10) \\ & =-10 \end{aligned}}$
(Jawaban B)
Soal Nomor 18
Jika $x \neq y$ memenuhi persamaan $5x \cdot \! ^3 \log 2^y = x \cdot \! ^3 \log 2^x + y \cdot \! ^3 \log 2^{4y}$, maka nilai $\dfrac{x}{y}$ adalah $\cdots \cdot$
A. $1$ C. $3$ E. $5$
B. $2$ D. $4$
Sederhanakan persamaan yang diberikan.
$$\begin{aligned} 5x~^3 \log 2^y & = x~^3 \log 2^x + y~^3 \log 2^{4y} \\ 5xy ~\cancel{^3 \log 2} & = x^2~\cancel{^3 \log 2} + 4y^2~\cancel{^3 \log 2} \\ 5xy & = x^2 + 4y^2 \\ x^2-5xy + 4y^2 & = 0 \\ (x-y)(x-4y) & = 0 \end{aligned}$$Persamaan terakhir menunjukkan bahwa $x = y$ atau $x = 4y$, tetapi karena diberikan bahwa $x \neq y$ (pada soal), maka dipilih $x = 4y$. Dengan demikian,
$\boxed{\dfrac{x}{y} = \dfrac{4y}{y} = 4}$
(Jawaban D)
Soal Nomor 19
Jika $b > 1, x > 0$ dan $(2x)^{^b \log 2} = (3x)^{^b \log 3}$, maka $x = \cdots \cdot$
A. $\dfrac{1}{216}$ C. $1$ E. $216$
B. $\dfrac16$ D. $6$
Logaritmakan kedua ruas, kemudian sederhanakan dengan menggunakan sifat-sifat logaritma.
$$\begin{aligned} (2x)^{^b \log 2} & = (3x)^{^b \log 3} \\ ^b \log (2x)^{^b \log 2} & = \! ^b \log (3x)^{^b \log 3} \\ ^b \log 2 \cdot \! ^b \log 2x & = \! ^b \log 3 \cdot \! ^b \log 3x \\ ^b \log 2 \cdot (^b \log 2 + \! ^b \log x) & = \! ^b \log 3 \cdot (^b \log 3 + \! ^b \log x) \\ (^b \log 2)^2 + ^b \log 2 \cdot \! ^b \log x & = (^b \log 3)^2 + \! ^b \log 3 \cdot \! ^b \log x \\ (^b \log 2)^2-(^b \log 3)^2 &= \! ^b \log 3 \cdot \! ^b \log x- \! ^b \log 2 \cdot \! ^b \log x \\ (^b \log 2 + \! ^b \log 3)(^b \log 2-\! ^b \log 3) & = \! ^b \log x(^b \log 3- \! ^b \log 2) \\ ^b \log 6 \cdot \cancel{^b \log \dfrac23} & = ^b \log x \cdot (-1) \cancel{^b \log \dfrac23} \\ \cancel{^b \log} 6 & = \cancel{^b \log} x^{-1} \\ x^{-1} & = 6 \\ x & = \dfrac16 \end{aligned}$$Jadi, nilai dari $x$ adalah $\boxed{\dfrac16}$
(Jawaban B)
Soal Nomor 20
Jika $x$ dan $y$ memenuhi $^2 \log x^2 + \! ^3 \log \dfrac{1}{y^3} = 4$ dan $^2 \log x + \! ^3 \log y^4 = 13$, maka nilai dari $^4 \log x- \! ^9 \log y = \cdots \cdot$
A. $\dfrac12$ C. $\dfrac52$ E. $\dfrac92$
B. $\dfrac32$ D. $\dfrac72$
Kedua persamaan logaritma di atas membentuk sistem persamaan yang dapat ditulis menjadi berikut.
$$\begin{cases} 2 \cdot ^2 \log x -3 ^3 \log y & = 4 \\ ^2 \log x + 4 \cdot \! ^3 \log y & = 13 \end{cases}$$Misalkan $^2 \log x = a$ dan $^3 \log y = b$ sehingga diperoleh SPLDV:
$$\begin{cases} 2a-3b & = 4 && (\cdots 1) \\ a+4b & = 13 && (\cdots 2) \end{cases}$$Selesaikan, kita peroleh $a = 5$ dan $b = 2$. Dengan demikian, substitusi balik menghasilkan
$$\begin{aligned} ^2 \log x = 5 & \Rightarrow x = 2^5 \\ ^3 \log y = 2 & \Rightarrow y = 3^2 \end{aligned}$$Jadi, kita peroleh
$$\boxed{\begin{aligned} ^4 \log x- \! ^9 \log y & = \! ^4 \log 2^5- \! ^9 \log 3^2 \\ & = \dfrac52-1 = \dfrac32 \end{aligned}}$$ (Jawaban B)
Soal Nomor 21
Diketahui $x_1$ dan $x_2$ adalah akar-akar persamaan $^2 \log (4^x + 6) = 3 + x$. Nilai dari $x_1 + x_2$ adalah $\cdots \cdot$
A. $^2 \log 3$ D. $^2 \log 72$
B. $^2 \log 6$ E. $^2 \log 312$
C. $3$
Diketahui $^2 \log (4^x + 6) = 3 + x.$
Dengan mengubah bentuk logaritma di atas menjadi bentuk pangkat, kita akan peroleh
$$\begin{aligned} 4^x + 6 & = 2^{3 + x} \\ (2^x)^2 + 6 & = 2^3 \cdot 2^x \\ (2^x)^2 + 6 & = 8 \cdot 2^x \end{aligned}$$Selanjutnya, misalkan $2^x = a$ sehingga diperoleh
$$\begin{aligned} a^2 + 6 & = 8a \\ a^2-8a+6 & = 0 \end{aligned}$$Hasil kali akar dari persamaan kuadrat terakhir adalah
$$\begin{aligned} a_1 \cdot a_2 & = \dfrac{\text{Konst}\text{anta}}{\text{Koef}\text{isien}~a^2} \\ 2^{x_1} \cdot 2^{x_2} & = \dfrac{6}{1} \\ 2^{x_1 + x_2} & = 6 \\ x_1 + x_2 & = \! ^2 \log 6 \end{aligned}$$Jadi, nilai dari $x_1 + x_2$ adalah $\boxed{^2 \log 6}$
(Jawaban B)
Soal Nomor 22
Nilai $x$ yang memenuhi persamaan $4^{\log x}-3 \cdot 2^{1+\log x} + 8 = 0$ adalah $\cdots \cdot$
A. $1$ atau $3$
B. $2$ atau $4$
C. $2$ atau $8$
D. $1$ atau $10$
E. $10$ atau $100$
Diketahui $4^{\log x}-3 \cdot 2^{1+\log x} + 8 = 0.$
Perhatikan bahwa persamaan di atas dapat ditulis menjadi
$$\begin{aligned} (2^2)^{\log x}-3 \cdot 2 \cdot 2^{\log x} + 8 & = 0 \\ \left(2^{\log x}\right)^2-6 \cdot 2^{\log x} + 8 & = 0 \end{aligned}$$Misalkan $2^{\log x} = a$, maka diperoleh persamaan kuadrat
$$\begin{aligned} a^2-6a+8 & = 0 \\ (a-2)(a-4) & = 0 \end{aligned}$$Diperoleh $a = 2$ atau $a = 4$.
Untuk $a = 2^{\color{red}{\log x}} = 2 = 2^{\color{red}{1}}$, kita peroleh $\color{red}{\log x = 1} \Rightarrow x = 10$.
Untuk $a = 2^{\color{blue}{\log x}} = 4 = 2^{\color{blue}{2}}$, kita peroleh $\color{blue}{\log x = 2} \Rightarrow x = 10^2 = 100$.
Jadi, nilai $x$ yang memenuhi persamaan $4^{\log x}-3 \cdot 2^{1+\log x} + 8 = 0$ adalah $\boxed{10~\text{atau}~100}$
(Jawaban E)
Soal Nomor 23
Diketahui $a$ dan $b$ adalah bilangan bulat positif yang tidak sama dengan $1$ sehingga $$^a \log x \cdot \! ^b \log x = \! \dfrac{^x \log b}{^x \log a}.$$Nilai $(a+b)x$ adalah $\cdots \cdot$
A. $ab+b^2$ atau $\dfrac{a}{b}+1$
B. $a^2b + ab$ atau $\dfrac{a^2}{b}+a$
C. $ab+a^2$ atau $\dfrac{b}{a}+1$
D. $ab+ab^2$ atau $\dfrac{b^2}{a}+a$
E. $2a+2b^2$ atau $\dfrac{a+b}{2}$
Gunakan sifat logaritma berikut.
$$\boxed{^a \log b = \! \dfrac{^c \log b}{^c \log a}}$$Kita peroleh
$$\begin{aligned} ^a \log x \cdot \! ^b \log x & = \! \dfrac{^x \log b}{^x \log a} \\ \dfrac{\log x}{\cancel{\log a}} \cdot \dfrac{\log x}{\log b} & = \dfrac{\log b}{\cancel{\log a}} \\ (\log x)(\log x) & = (\log b)(\log b) \\ (\log x)^2 & = (\log b)^2 \end{aligned}$$Ada dua kemungkinan yang memenuhi persamaan logaritma di atas.
Kemungkinan pertama:
$$\log x = \log b \Rightarrow x = b$$sehingga
$$\begin{aligned} (a+b)x & = (a+b)b \\ & = ab + b^2 \end{aligned}$$ Kemungkinan kedua:
$$\log x = -\log b \Rightarrow x = b^{-1}$$sehingga
$$\begin{aligned} (a+b)x & = (a+b)b^{-1} \\ & = \dfrac{a}{b}+1 \end{aligned}$$Jadi, nilai $(a+b)x$ adalah $$\boxed{ab+b^2~\text{atau}~\dfrac{a}{b}+1}$$ (Jawaban A)
Soal Nomor 24
Misalkan $x_0$ adalah penyelesaian dari persamaan $2^{3 \cdot \! \log x} \cdot 5^{\log x} = 1.600$. Jumlah digit penyusun bilangan $x_0$ adalah $\cdots \cdot$
A. $0$ C. $2$ E. $5$
B. $1$ D. $4$
Dengan menggunakan sifat-sifat eksponen dan logarjtma, kita akan memperoleh
$$\begin{aligned} 2^{3 \cdot \! \log x} \cdot 5^{\log x} & = 1.600 \\ \left(2^{\log x}\right)^3 \cdot 5^{\log x} & = 1.600 \\ \left(2^{\log x}\right)^2 \cdot 2^{\log x} \cdot 5^{\log x} & = 1.600 \\ \left(2^{\log x}\right)^2 \cdot 10^{\log x} & = 1.600 \\ \left(2^{\log x}\right)^2 \cdot x & = 1.600 && (a^{^a \log b} = b) \\ \log \left[\left(2^{\log x}\right)^2 \cdot x\right] & = \log 1.600 && (\text{Tarik Logari}\text{tma}) \\ \log \left(2^{\log x}\right)^2 + \log x & = \log 1.600 \\ 2 \log x \log 2 + \log x & = \log 1.600 \\ \log x(2 \log 2 + 1) & = \log 1.600 \\ \log x(\log 2^2 + \log 10) & = \log 1.600 \\ \log x(\log 40) & = \log 1.600 \\ \log x & = \dfrac{\log 1.600}{\log 40} = ^{40} \log 1.600 = 2 \\ x & = 10^2 = 100 \end{aligned}$$Jadi, penyelesaian persamaan logaritma itu adalah $x_0 = 100$ dengan jumlah digit penyusunnya adalah $\boxed{1+0+0 = 1}$
(Jawaban B)
Soal Nomor 25
Jumlah dari semua bilangan $x$ sehingga $^2 \log (x^2-4x-1)$ merupakan bilangan bulat adalah $\cdots \cdot$
A. $0$ C. $2$ E. $6$
B. $1$ D. $4$
Misalkan $^2 \log (x^2-4x-1) = p$ untuk suatu bilangan bulat $p \geq 0$ sehingga bila diubah menjadi bentuk pangkat, diperoleh $x^2-4x-1 = 2^p$. Perhatikan bahwa $p$ tidak mungkin negatif karena kita tahu bahwa $x^2-4x-1$ pasti bulat ketika $x$ bulat.
Selanjutnya,
$$\begin{aligned} \left[(x-2)^2-4\right]-1 & = 2^p \\ (x-2)^2-5 & = 2^p \\ (x-2)^2 & = 2^p + 5 \end{aligned}$$Misalkan $2^p + 5 = a^2$.
Jelas $a$ ganjil sehingga $a = 2k + 1$ untuk suatu bilangan bulat $k$.
Kita tuliskan
$$\begin{aligned} 2^p + 5 & = (2k + 1)^2 \\ 2^p + 5 & = 4k^2+4k+1 \\ 2^p & =4k^2+4k-4 \\ 2^p & = 4(k^2+k-1) \end{aligned}$$Berarti $2^p$ habis dibagi $4$ sehingga $p \geq 2$.
Kita juga dapat tuliskan
$$2^{p-2} = k^2+k-1$$Perhatikan bahwa berapa pun nilai $k$, ruas kanan selalu bernilai ganjil sehingga ruas kiri juga harus demikian.
Akibatnya, $2^{p-2} = 1$ (satu-satunya hasil perpangkatan $2$ yang ganjil).
Akhirnya, kita peroleh $p = 2$.
Untuk $p = 2$, diperoleh
$$\begin{aligned} x^2-4x-1 & = 2^2 \\ x^2-4x-5 & = 0 \\ (x-5)(x+1) & = 0 \end{aligned}$$Diperoleh $x_0 = -1$ atau $x_1 = 5$. Kedua penyelesaian bulat ini dapat diterima karena substitusi membuat numerus bernilai positif.
Jadi, jumlah semua nilai $x$ yang dimaksud adalah $\boxed{x_0+x_1 = (-1) + 5 = 4}$
(Jawaban D)
Soal Nomor 26
Jika $x_1$ dan $x_2$ memenuhi persamaan $^2 \log x^{1 + \! ^2 \log x} = 2,$ maka nilai $x_1 + x_2 = \cdots \cdot$
A. $2\dfrac14$ D. $4\dfrac12$
B. $2\dfrac12$ E. $6\dfrac14$
C. $4\dfrac14$
Perhatikan bahwa variabel $x$ muncul dalam bentuk $^2 \log x.$ Oleh karena itu, kita misalkan $^2 \log x = y$ sehingga $x = 2^y.$ Selanjutnya, tinggal sederhanakan persamaannya.
$$\begin{aligned} ^2 \log x^{1 + \! ^2 \log x} & = 2 \\ (1 + \! ^2 \log x) \cdot \! ^2 \log x & = 2 \\ (1 + \! ^2 \log 2^y) \cdot \! ^2 \log 2^y & = 2 \\ (1 + y) \cdot y & = 2 \\ y^2 + y-2 & = 0 \\ (y+2)(y-1) & = 0 \\ y_1 = -2~\text{atau}~y_2 & = 1 \end{aligned}$$Karena $x = 2^y,$ maka kita peroleh
$$\begin{aligned} x_1 + x_2 & = 2^{y_1} + 2^{y_2} \\ & = 2^{-2} + 2^1 \\ & = \dfrac14 + 2 \\ & = 2\dfrac14 \end{aligned}$$Jadi, nilai dari $\boxed{x_1+x_2=2\dfrac14}$
(Jawaban A)
Bagian Uraian
Soal Nomor 1
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut.
a. $^2 \log x = \! ^2 \log 15$
b. $^2 \log (4x) = 2$
Jawaban a)
Diketahui $^2 \log x = \! ^2 \log 15$.
Karena bilangan pokok (basis) sudah sama, maka kita langsung peroleh $\boxed{x = 15}$
Jawaban b)
Diketahui $^2 \log (4x) = 2$.
Dari sini, kita peroleh
$$\begin{aligned} 4x & = 2^2 \\ 4x & = 4 \\ x & = 1 \end{aligned}$$Jadi, nilai $\boxed{x = 1}$
Soal Nomor 2
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut.
a. $^c \log x^2 = \! ^c \log (4x-4)$
b. $^p \log (x^2-12) = \! ^p \log x$
Jawaban a)
Diketahui $^c \log x^2 = \! ^c \log (4x-4).$
Karena basisnya sudah sama, maka kita peroleh persamaan pada bagian numerus.
$$\begin{aligned} x^2 & = 4x-4 \\ x^2-4x+4 & = 0 \\ (x-2)^2 & = 0 \end{aligned}$$Diperoleh $\boxed{x = 2}$
Jawaban b)
Diketahui $^p \log (x^2-12) = \! ^p \log x.$
Karena basisnya sudah sama, maka kita peroleh persamaan pada bagian numerus.
$$\begin{aligned} x^2-12 & = x \\ x^2-x-12 & = 0 \\ (x-4)(x+3) & = 0 \end{aligned}$$Diperoleh dua nilai $x$, yaitu $x = 4$ atau $x = -3$, tetapi perhatikan bahwa substitusi $x = -3$ membuat numerus bernilai negatif sehingga penyelesaian ini ditolak.
Jadi, nilai $x$ yang memenuhi adalah $\boxed{x = 4}$
Soal Nomor 3
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut.
a. $^2 \log x + \! ^2 \log (x-6) = 4$
b. $^5 \log (2x+4)- \! ^5 \log (x-1) = 1$
Jawaban a)
Diketahui $^2 \log x + \! ^2 \log (x-6) = 4.$
Gunakan sifat penjumlahan logaritma, lalu selesaikan.
$$\begin{aligned} ^2 \log \left[x(x-6)\right] & = 4 \\ x(x-6) & = 2^4 \\ x^2-6x & = 16 \\ x^2-6x-16 & = 0 \\ (x-8)(x+2) & = 0 \end{aligned}$$Diperoleh dua nilai $x$, yaitu $x = 8$ atau $x = -2$, tetapi perhatikan bahwa substitusi $x = -2$ membuat numerus bernilai negatif sehingga penyelesaian ini ditolak.
Jadi, nilai $x$ yang memenuhi adalah $\boxed{x = 8}$
Jawaban b)
Diketahui $^5 \log (2x+4)- \! ^5 \log (x-1) = 1.$
Gunakan sifat pengurangan logaritma, lalu selesaikan.
$$\begin{aligned} ^5 \log \dfrac{2x+4}{x-1} & = 1 \\ \dfrac{2x+4}{x-1} & = 5^1 \\ 2x+4 & = 5(x-1) \\ 2x+4 & = 5x-5 \\ 3x & = 9 \\ x & = 3 \end{aligned}$$Jadi, nilai $x$ yang memenuhi adalah $\boxed{x = 3}$
Soal Nomor 4
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut.
$$\log x + \log (x+1) = \log 2$$
Diketahui $\log x + \log (x+1) = \log 2.$
Gunakan sifat penjumlahan logaritma, lalu selesaikan.
$$\begin{aligned} \log \left[x(x+1)\right] & = \log 2 \\ x(x+1) & = 2 \\ x^2+x & = 2 \\ x^2+x-2 & = 0 \\ (x+2)(x-1) & = 0 \end{aligned}$$Diperoleh dua nilai $x$, yaitu $x = -2$ atau $x = 1$, tetapi perhatikan bahwa substitusi $x = -2$ membuat numerus bernilai negatif sehingga penyelesaian ini ditolak.
Jadi, nilai $x$ yang memenuhi adalah $\boxed{x = 1}$
Soal Nomor 5
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut.
$$\log (x-3) + \log (x-2) = \log (2x+24)$$
Diketahui $$\log (x-3) + \log (x-2) = \log (2x+24).$$Gunakan sifat penjumlahan logaritma, lalu selesaikan.
$$\begin{aligned} \log \left[(x-3)(x-2)\right] & = \log (2x+24) \\ (x-3)(x-2) & = 2x+24 \\ x^2-5x+6 & = 2x+24 \\ x^2-7x-18 & = 0 \\ (x-9)(x+2) & = 0 \end{aligned}$$Diperoleh dua nilai $x$, yaitu $x = 9$ atau $x = -2$, tetapi perhatikan bahwa substitusi $x = -2$ membuat numerus bernilai negatif sehingga penyelesaian ini ditolak.
Jadi, nilai $x$ yang memenuhi adalah $\boxed{x = 9}$
Soal Nomor 6
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut untuk $x > 0$.
$$^{\frac{4}{x}} \log (x^2-6) = 2$$
Diketahui $^{\frac{4}{x}} \log (x^2-6) = 2.$
Dengan mengubah bentuk logaritma di atas menjadi bentuk pangkat, diperoleh
$$\begin{aligned} x^2-6 & = \left(\dfrac{4}{x}\right)^2 \\ x^2-6 & = \dfrac{16}{x^2} \\ \text{Kalikan kedua}~&\text{ruas dengan}~x^2 \\ x^4-6x^2 & = 16 \\ x^4-6x^2-16 & = 0 \\ (x^2-8)(x^2+2) & = 0 \end{aligned}$$Diperoleh $$x^2 = 8 \Rightarrow x = \pm 2\sqrt2$$atau $$x^2 = -2 \Rightarrow x = \emptyset$$Karena $x > 0$, maka satu-satunya penyelesaian persamaan logaritma tersebut adalah $\boxed{x = 2\sqrt2}$
Soal Nomor 7
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut.
a. $^3 \log ^3 \log x = 1$.
b. $\log \log x = 2$.
Jawaban a)
Diketahui $^3 \log \color{blue}{^3 \log x} = 1$.
Ubah bentuk logaritma di atas menjadi bentuk pangkat (prosesnya dua kali).
$$\begin{aligned} \color{blue}{^3 \log x} & = 3^1 = 3 \\ x & = 3^3 = 27 \end{aligned}$$Jadi, nilai $x$ yang memenuhi persamaan itu adalah $\boxed{x=27}$
Jawaban b)
Diketahui $\log \color{blue}{\log x} = 2$.
Perhatikan bahwa bila bilangan pokok (basis) pada bentuk logaritma tidak ditulis, maka itu artinya nilai basisnya $10$.
Ubah bentuk logaritma di atas menjadi bentuk pangkat (prosesnya dua kali).
$$\begin{aligned} \log x & = 10^2 = 100 \\ x & = 10^{100} \end{aligned}$$Jadi, nilai $x$ yang memenuhi persamaan itu adalah $\boxed{x=10^{100}}$
Soal Nomor 8
Carilah nilai $x$ yang memenuhi persamaan logaritma berikut.
a. $^3 \log x^3 = \! ^3 \log^2 x$.
b. $^2 \log^2 x = 9$.
Jawaban a)
Diketahui $^3 \log x^3 = \! ^3 \log^2 x$.
Perhatikan bahwa persamaan logaritma di atas dapat kita tulis menjadi
$$\begin{aligned} 3 \cdot \! ^3 \log x-\! ^3 \log^2 x & = 0 \\ ^3 \log x(3-\! ^3 \log x) & = 0 \end{aligned}$$Diperoleh
$$\begin{aligned} ^3 \log x = 0 & \Rightarrow x = 3^0 = 1 \\ ^3 \log x = 3 & \Rightarrow x = 3^3 = 27 \end{aligned}$$Jadi, ada dua nilai $x$ yang memenuhi persamaan, yakni $\boxed{x=1~\text{atau}~x=27}$
Jawaban b)
Diketahui $^2 \log^2 x = 9$.
Tarik akar kuadrat dan kita peroleh
$$^2 \log x = \pm 3$$Dengan demikian, didapat
$$\begin{aligned} ^2 \log x = 3 & \Rightarrow x = 2^3 = 8 \\ ^2 \log x = -3 & \Rightarrow x = 2^{-3} = \dfrac18 \end{aligned}$$Jadi, ada dua nilai $x$ yang memenuhi persamaan itu, yakni $\boxed{x = 8~\text{atau}~x = \dfrac18}$
Soal Nomor 9
Carilah semua nilai $x$ yang memenuhi persamaan $^3 \log (5x+1) = \! ^9 \log (5(x+1)^2).$
Diketahui $^3 \log (5x+1) = \! ^9 \log (5(x+1)^2).$
Dari persamaan tersebut, samakan bilangan pokok (basis) dengan menguadratkan basis dan numerus pada bentuk logaritma di ruas kiri. Selanjutnya, kita gunakan persamaan numerusnya untuk mencari nilai $x$.
$$\begin{aligned} ^{3^2} \log (5x+1)^2 & = \! ^9 \log (5(x+1)^2) \\ ^{9} \log (5x+1)^2 & = \! ^9 \log (5(x+1)^2) \\ (5x+1)^2 & = 5(x+1)^2 \\ (5x+1)^2 & = (\sqrt5x + \sqrt5)^2 \\ (5x+1)^2-(\sqrt5x + \sqrt5)^2 & = 0 \\ (5x+1+\sqrt5x+\sqrt5)(5x+1-\sqrt5x-\sqrt5) & = 0 && (a^2-b^2 = (a+b)(a-b)) \end{aligned}$$Kita memperoleh dua kemungkinan.
Kemungkinan pertama:
$$\begin{aligned} 5x+1+\sqrt5x+\sqrt5 & = 0 \\ (5+\sqrt5)x & = -1-\sqrt5 \\ x & = -\dfrac{1+\sqrt5}{5+\sqrt5} \color{red}{\times \dfrac{5-\sqrt5}{5-\sqrt5}} && (\text{dirasionalkan}) \\ x & = \dfrac{5-\sqrt5+5\sqrt5-5}{25-5} \\ x & = -\dfrac{4\sqrt5}{20} = -\dfrac15\sqrt5 \end{aligned}$$Namun, nilai $x = -\dfrac15\sqrt5$ bila disubstitusi pada numerus logaritma $^3 \log (5x+1)$ menghasilkan nilai $5\left(-\dfrac15\sqrt5\right) + 1 = -\sqrt5 + 1$ (bertanda negatif) sehingga penyelesaian ini ditolak.
Kemungkinan kedua:
$$\begin{aligned} 5x+1-\sqrt5x-\sqrt5 & = 0 \\ (5-\sqrt5)x & = \sqrt5-1 \\ x & = -\dfrac{\sqrt5-1}{5-\sqrt5} \color{red}{\times \dfrac{5+\sqrt5}{5+\sqrt5}} && (\text{dirasionalkan}) \\ x & = \dfrac{5\sqrt5+5-5-\sqrt5}{25-5} \\ x & = \dfrac{4\sqrt5}{20} = \dfrac15\sqrt5 \end{aligned}$$Penyelesaian ini diterima karena substitusi pada numerus logaritma menghasilkan tanda positif.
Jadi, hanya ada $1$ nilai $x$ yang memenuhi persamaan logaritma tersebut, yaitu $\boxed{x = \dfrac15\sqrt5}$
Soal Nomor 10
Selesaikan persamaan logaritma berikut.
a. $10^{4 \log x}- 7\left(10^{2 \log x}\right) + 10 = 0$
b. $10^{6 \log x}-4\left(10^{3 \log x}\right)-12 = 0$
Jawaban a)
Diketahui $10^{^4 \log x}- 7\left(10^{^2 \log x}\right) + 10 = 0.$
Perhatikan bahwa persamaan di atas dapat ditulis menjadi
$$\begin{aligned} \left(10^{\log x}\right)^4- 7\left(10^{\log x}\right)^2 + 10 & = 0 \\ x^4-7x^2 + 10 & = 0 && (a^{^a \log b} = b) \\ (x^2-5)(x^2-2) & = 0 \end{aligned}$$Selanjutnya, kita peroleh
$$\begin{aligned} x^2 = 5 & \Rightarrow x = \pm \sqrt5 \\ x^2 = 2 & \Rightarrow x = \pm \sqrt2 \end{aligned}$$Perhatikan bahwa nilai $x = -\sqrt2$ atau $x = -\sqrt5$ membuat numerus logaritma bernilai negatif sehingga kedua penyelesaian ini ditolak.
Jadi, penyelesaian persamaan logaritma tersebut adalah $\boxed{x = \sqrt2~\text{atau}~x = \sqrt5}$
Jawaban b)
Diketahui $10^{6 \log x}-4\left(10^{3 \log x}\right)= 12.$
Perhatikan bahwa persamaan di atas dapat ditulis menjadi
$$\begin{aligned} \left(10^{\log x}\right)^6- 4\left(10^{\log x}\right)^3 -12 & = 0 \\ x^6-4x^3-12 & = 0 && (a^{^a \log b} = b) \\ (x^3-6)(x^3+2) & = 0 \end{aligned}$$Selanjutnya, kita peroleh
$$\begin{aligned} x^3 = 6 & \Rightarrow x = \sqrt[3]{6} \\ x^3 = -2 & \Rightarrow x = \sqrt[3]{-2} \end{aligned}$$Perhatikan bahwa nilai $x = \sqrt[3]{-2}$ membuat numerus logaritma bernilai negatif sehingga penyelesaian ini ditolak.
Jadi, penyelesaian persamaan logaritma tersebut adalah $\boxed{x = \sqrt[3]{6}}$
Soal Nomor 11
Selesaikan persamaan logaritma berikut.
$$^4 \log x = \! ^x \log 256$$
Diketahui $^4 \log x = \! ^x \log 256.$
Perhatikan bahwa persamaan logaritma di atas dapat ditulis menjadi
$$\begin{aligned} ^4 \log x & = \! ^x \log 4^4 \\ ^4 \log x & = 4 \cdot \! ^x \log 4 \\ ^4 \log x & = 4 \cdot \dfrac{1}{^4 \log x} \end{aligned}$$Misalkan $^4 \log x = a$, maka kita peroleh
$$\begin{aligned} a & = 4 \cdot \dfrac{1}{a} \\ a^2 & = 4 \\ a & = \pm 2 \end{aligned}$$Untuk $a = 2$, diperoleh $^4 \log x = 2$ sehingga $x = 4^2 = 16$.
Untuk $a = -2$, diperoleh $^4 \log x = -2$ sehingga $x = 4^{-2} = \dfrac{1}{16}$.
Jadi, penyelesaian persamaan logaritma tersebut adalah $\boxed{x=\dfrac{1}{16}~\text{atau}~x = 16}$
Soal Nomor 12
Selesaikan persamaan logaritma berikut.
$$^x \log (5x^3-4x) = \!^x \log x^5$$
Diketahui $^x \log (5x^3-4x) = ^x \log x^5.$
Karena bilangan pokok (basis) logaritma sudah sama, maka kita bisa langsung ambil persamaan numerusnya.
$$\begin{aligned} 5x^3-4x & = x^5 \\ x^5-5x^3+4x & = 0 \\ x(x^4-5x^2+4) & = 0 \\ x\color{red}{(x^2-4)}\color{blue}{(x^2-1)} & = 0 \\ x\color{red}{(x+2)(x-2)}\color{blue}{(x+1)(x-1)} & = 0 \end{aligned}$$Dari persamaan terakhir, diperoleh $5$ nilai $x$, yaitu $\{-2, -1, 0, 1, 2\}$. Namun, nilai $x = -2$, $x = -1$, $x = 0$, atau $x = 1$ keempatnya tidak memenuhi syarat bahwa basis harus positif dan tidak sama dengan $1$, serta numerus juga harus positif. Dengan kata lain, hanya $x=2$ yang memenuhi semua syarat.
Jadi, penyelesaian persamaan logaritma tersebut adalah $\boxed{x=2}$
Soal Nomor 13
Anggap bahwa $a$ dan $b$ merupakan bilangan positif berbeda yang memenuhi $a^b = b^a$ dan $b = 9a$. Berapakah nilai $a$?
Diketahui $a^b = b^a$.
Karena bilangan pokok (basis) berbeda, maka satu-satunya cara untuk menurunkan eksponen adalah menarik logaritma pada kedua ruas.
$$\begin{aligned} a^b & = b^a \\ \log a^b & = \log b^a \\ \color{red}{b} \log a & = a \log \color{red}{b} \\ \text{Substitusi}~b & = 9a \\ 9\cancel{a} \log a & = \cancel{a} \log 9a \\ 9 \log a & = \log 9a \\ \log a^9 & = \log 9a \\ a^9 & = 9a \\ a(a^8-9) & = 0 \\ a = 0~\text{atau}~a^8 & = 9 \end{aligned}$$Karena $a$ diketahui adalah bilangan positif, maka nilai $a = 0$ ditolak.
Dengan demikian,
$$\begin{aligned} a^8 & = 9 \\ a^8 & = 3^2 \\ a & = 3^{2/8} = 3^{1/4} = \sqrt[4]{3} \end{aligned}$$Jadi, nilai $\boxed{a = \sqrt[4]{3}}$
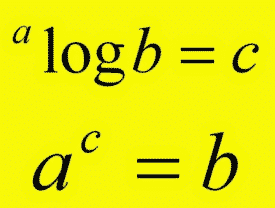
Posting Komentar